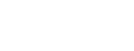
La Temperatura según la Teoría Cinética
Vamos a partir de la ecuación que hemos obtenido para la presión:
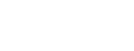 |
Es posible comprender mejor el significado de la temperatura si escribimos la ecuación anterior como:
Comparándola con la ecuación de estado de un gas ideal:
| PV = NkBT |
De aquí encontramos que
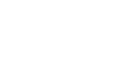 |
Podemos despejar la energía cinética molecular como:
Puesto que ![]() , se concluye que
, se concluye que
El siguiente teorema, llamado el teorema de la
equipartición de la energía, establece que:
La energía de un sistema en equilibrio térmico se divide por igual
entre todos los grados de libertad.
La energía cinética traslacional de N moléculas es simplemente N veces la energía promedio por molécula, entonces:
La raíz cuadrada de ![]() se
conoce como velocidad cuadrática media de las moléculas (rms,
por sus siglas en inglés). Para la velocidad rms tenemos:
se
conoce como velocidad cuadrática media de las moléculas (rms,
por sus siglas en inglés). Para la velocidad rms tenemos:
 |
Gas |
Masa molecular g/mol) |
vrms a 20ºC (m/s) |
H2 |
2.02 |
1902 |
He
|
4 |
1352 |
H2O
|
18 |
637 |
Ne |
20.1 |
603 |
N2 |
28 |
511 |
NO |
30 |
494 |
CO2 |
44 |
408 |
SO2 |
64 |
338 |