El aprendizaje de la física y la
resolución de problemas
La física pretende describir y explicar unos determinados fenómenos
mediante la creación de una serie de conceptos y teorías.
Esos conceptos y teorías se corresponden, de algún modo
con los fenómenos. Se dice que “representan” esos fenómenos.
Vemos pues que existen dos niveles, el de la realidad y el conceptual
y cuando estemos manejando la Física, ya sea aprendiéndola
o aplicándola, siempre tendremos que tener presentes los dos niveles.
Resulta, en la mayoría de las ocasiones más fácil
y cómodo trabajar con las teorías (en el nivel conceptual)
y predecir con ellas el comportamiento de las cosas (en el plano de la
realidad). Imaginemos que deseamos construir un gran puente de varios
cientos de metros de largo. Si no tenemos una teoría suficientemente
segura del comportamiento de los materiales, podríamos construirlo
empleando una gran cantidad de materiales para estar seguros de que resistirá
o podríamos tratar de ahorrar el máximo, con lo cual, posiblemente
no resistirá. Si tenemos la teoría adecuada, podemos hacer
los cálculos y construir el puente más económico
y suficientemente resistente porque hay una correspondencia entre lo que
predice esa teoría y el comportamiento de los puentes.
Decimos que los conceptos y las relaciones tienen un significado. Establecer
la relación de significación (x) de una clase de expresiones
(y) consiste en asociar dicha clase de expresiones con un conjunto de
propiedades (a, b, c) que delimitan lo que se denomina el significado
(x) de (y). Mediante la relación de significación se establece
una correspondencia entre lo que representa y lo representado, válida
para cualquier destinatario posible. También se debe destacar que
el significado de una expresión es susceptible de interpretación,
no es algo que todos lo comprendan y acepten del mismo modo.
Para resolver un problema, debemos representarlo en el nivel conceptual
y esto ha de hacerse, por una parte, tomando información del enunciado,
y por otra, utilizando también una serie de conocimientos sobre
la realidad inmediata de las cosas y sobre la teoría física
relacionada con el problema, que se han debido adquirir previamente.
En muchas ocasiones el significado que el alumno utiliza es un significado
propio, relacionado con sus ideas previas, o con sus errores conceptuales.
También existe la posibilidad de que no le dé importancia
al significado, al menos en la práctica, sino que pase directamente
del enunciado a las fórmulas de un modo, pretendidamente mecánico,
que podríamos denominar "utilización ciega de fórmulas"
y que es una actuación bastante habitual.
|
Ejemplo comentado de resolución
de problemas con estrategias
Disponemos de un miliamperímetro de 5 Ω de resistencia interna, que es capaz de medir hasta 8 mA. Calcula la resistencia que se le debe conectar, para transformarlo en amperímetro que mida hasta 8 A.
|
Vamos a explicar este punto mediante su aplicación en otro problema en el que resulta más claro su significado.
|
Continuamos con la aplicación del punto 1 al problema de electricidad que nos ocupa.
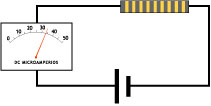
En este problema es imprescindible conocer un mínimo de aspectos teóricos para hacernos idea del fenómeno o situación descrito en el enunciado:
• El amperímetro es un aparato de medida que se conecta en serie, de tal modo que pase por él toda la corriente cuya intensidad se desea medir.
 |
• Cuando le conectamos la resistencia incógnita, el nuevo
amperímetro está formado por el anterior y la nueva resistencia
en paralelo y por lo tanto por todo ese conjunto es por donde han de pasar
los 8 A.
|
Podemos representar los aspectos más básicos de las dos situaciones de las que nos habla el enunciado del problema de la siguiente forma:
 |
Acabamos de ver que para hacernos una mejor idea de la situación,
es muy importante hacer una representación gráfica, que
era uno de los puntos de las estrategias
|
También era muy importante, la cuestión del significado de los conceptos, en este caso, por el amperímetro ha de pasar toda la corriente y por tanto los 8 amperios pasarán por el conjunto formado por el inicial y la resistencia en paralelo. Y cuando la intensidad total sea 8 A, por el miliamperímetro pasarán los 8 m A, que es lo máximo que puede pasar por él.
Notemos que esta última idea “cuando la intensidad total sea 8 A, por el miliamperímetro pasarán los 8 m A, que es lo máximo que puede pasar por él”, la obtengo de la comprensión del comportamiento del amperímetro, no de ninguna fórmula, y es básica para la resolución del problema.
|
Partiendo de la comprensión de la situación, del significado
de los conceptos y del conocimiento de las leyes, buscamos las leyes que
se ajustan.
En esta situación es mejor el esquema gráfico en el que
se muestra el amperímetro inicial como una resistencia de 5 Ω.
 |
Las leyes adecuadas son las siguientes:
• La intensidad de la corriente que llega a un nudo es la suma de
las que salen de él
• Entre dos puntos hay una diferencia de potencial única,
esto es, si hay dos resistencias en paralelo, la diferencia de potencial
entre los extremos de las mismas es única.
• La ley de Ohm.
|
En este caso tiene poca dificultad, pero, en general, se trata de hacer una reflexión consciente sobre las condiciones de aplicación de las leyes. Hay otros problemas en los que esta reflexión tiene más importancia, por ejemplo en un problema en el que nos planteamos la aplicación de la conservación de la energía mecánica hay que ser consciente de que no actúa ninguna fuerza no conservativa, como rozamiento, motores, etc.
|
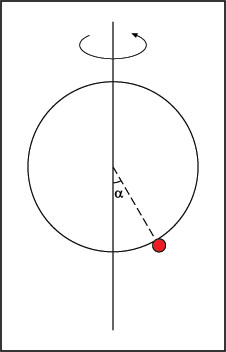
Se trata de hacer una reflexión consciente, en este caso de que no nos dejamos ningún concepto y que todos son los apropiados. En el problema que nos ocupa, volver a reflexionar sobre las intensidades. En el problema que hemos indicado antes, de la bola ensartada en un anillo que gira, se trataría aquí de reflexionar de nuevo sobre las fuerzas y la aceleración. La aceleración debe tener la dirección de un radio de la circunferencia descrita y dirigida hacia dentro. Las fuerzas deben ser la que hace la Tierra, el peso, y la que hace el anillo, que como no hay rozamiento y por tanto no puede haber componente tangencial, debe ser perpendicular al anillo (radial) y dirigida hacia dentro.
|
8 = 0´008 + IR → Intensidad que entra = suma de
las intensidades que salen
0´008.5 = IR. R → Diferencia de potencial en la
r del miliamperímetro = diferencia de potencial en la r incógnita
Luego
0´008.5 = (8 - 0´008).R
Despreciando 0´008 frente a 8, queda:
R = 0´008.5/8 = 0´005 Ω
|
Podemos hacer varias reflexiones:
Por la resistencia incógnita debe pasar mucha más intensidad que por la del miliamperímetro, entonces debe ser mucho más pequeña.
El amperímetro en su conjunto debe tener una resistencia pequeña,
ya que se conecta en serie con el resto del circuito, entonces, la nueva
resistencia será la que tenía antes el circuito más
la del amperímetro. Como el circuito con amperímetro debe
tener una resistencia, lo más parecida posible al circuito sin
amperímetro, la del amperímetro debe ser pequeña.
Al conectar la resistencia incógnita en paralelo, conseguimos una
resistencia más pequeña que la inicial del miliamperímetro.
Ejercicio propuesto
para reflexionar sobre estrategias de aprendizaje:
Un voltímetro de 105 Ω de resistencia
interna es capaz de medir hasta 20 mV. Calcula la resistencia que se le
debe conectar, para transformarlo en voltímetro que mida hasta
200 V.