Ejercicios

2. CIRCUITOS

Ej2.1. Indica qué bombillas estarán encendidas en los siguientes circuitos:

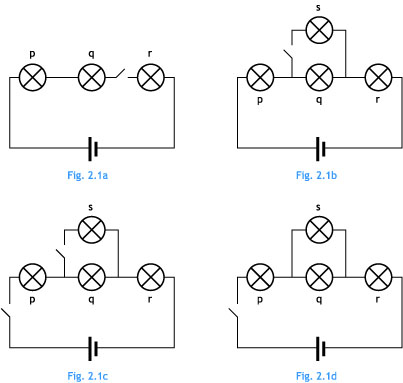3. SUSTANCIAS CONDUCTORAS

Ej3.1. En el circuito de la figura, intercalamos entre a y b objetos de diversos materiales

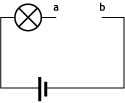¿De entre los siguientes materiales, con cuáles crees que lucirá la bombilla? Da algún motivo de tu respuesta
Cobre, hierro, plástico, vidrio, goma.

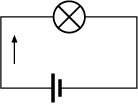
Ej3.2. Un diodo es un dispositivo que no es simétrico en su comportamiento. Una bombilla lucirá de la misma manera si conectamos su extremo inferior al polo positivo de la pila que si lo conectamos al casquillo.

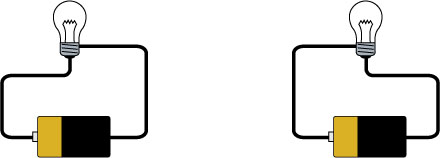Un diodo no se comporta así.

Dadas las hipótesis siguientes ¿cuál de ellas crees que debe ser eliminada por la experiencia de los circuitos de la figura?:
a) Por cada terminal de la pila sale una corriente hacia la bombilla.

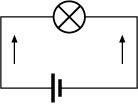b) La corriente sale de la pila por un terminal y entra por el otro.

4. EFECTOS

5. MEDIDAS

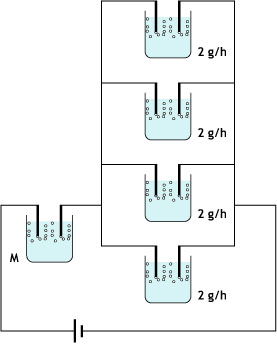
Ej5.1. Todas las cubas electrolíticas representadas son iguales.
a) ¿Qué cantidad de materia se depositará en la cuba M?
b) ¿Si por la cuba M pasa una corriente de 12 amperios, ¿cuál será la intensidad de la corriente por las demás?

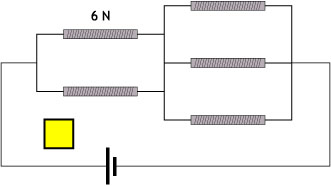
Ej5.2. Todos los electroimanes representados son iguales. Hay uno que ejerce una fuerza de 6 N sobre el bloque de hierro representado, en color amarillo, cuando se coloca en uno de sus extremos.

a) ¿Cuál será la fuerza que ejercerá cada electroimán sobre dicho bloque de hierro, cuando se coloque en uno de sus extremos?
b) Si definimos el amperio como la intensidad de la corriente que pasa por un electroimán como los de la figura, que ejerce una fuerza de 2 N sobre el bloque de hierro, ¿cuánto amperios pasarán por cada electroimán?
c) Si con otra corriente pasan 5 A por el electroimán situado más arriba de los tres que están en paralelo, ¿qué intensidad de corriente pasará por cada uno de los demás?

Ej5.3. Supongamos que se define el amperio como la intensidad de la corriente que hace que se depositen 3 g de la sustancia X por hora.
a) Si en un punto del circuito se depositan 12 g por hora, ¿cuántos amperios pasarán?
b) Si por una cuba pasan 18 amperios, ¿cuántos gramos de la sustancia X se depositarán?

6. NATURALEZA DE LA CORRIENTE

Ej6.1. Escribe un informe argumentando que la corriente está formada por cargas eléctricas, como las de los fenómenos electrostáticos. Ten en cuenta en la argumentación las Características de la Ciencia 1.

7. CONCEPTOS BÁSICOS

Intensidad de la corriente

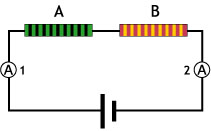
Ej7.1. El amperímetro 1 de la figura marca 6 A. ¿Cuánto marcará el 2?

Ej7.2. En el circuito de la figura el amperímetro 1 marca 8 A y el amperímetro 2 marca 3 A. ¿cuánto marcarán los otros amperímetros?

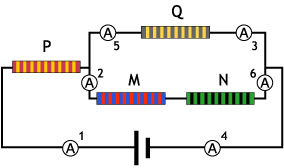Ej7.3. En el circuito de la figura, pasa por el punto b una corriente de 4 A y por n, otra corriente de 2 A. ¿Qué corriente pasará por los restantes puntos? Razona la respuesta.

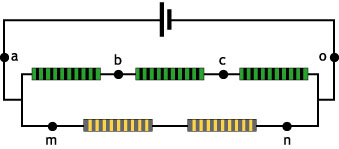Ej7.4. En el circuito de la figura pasan 8 A por el punto a y 2 A por el m.
¿Cuentos amperios pasarán por los restantes puntos marcados? Razona la respuesta

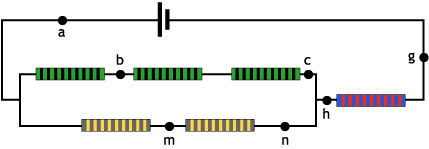Diferencia de potencial

Ej7.5. Considera el circuito de la figura 7.5b. ¿Cómo comprobarías que la energía que pierde la unidad de carga al pasar de uno a otro de sus terminales es la suma de la que pierde en A más la que pierde en B.

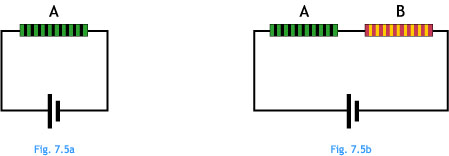Ej7.6. En los circuitos de las figuras 7.5a y 7.5b, los conductores que tienen el mismo nombre son iguales y las pilas también. ¿Crees que la unidad de carga disipará más energía cuando atraviese el conductor A, en el circuito de la figura 7.5a o en el de la figura 7.5b?. Justifica la respuesta.

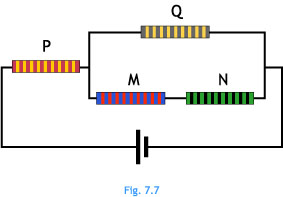
Ej7.7. En el circuito de la figura 7.7, ¿por donde crees que una carga perderá más energía, por M y N o por O?. Justifica la respuesta.

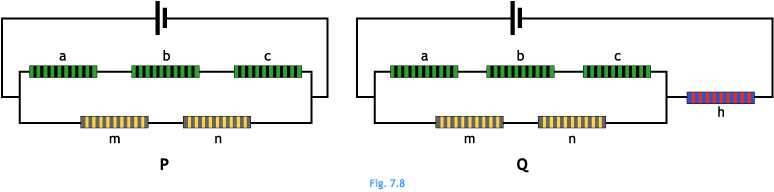
Ej7.8. En la figura 7.8 las dos pilas son iguales y los conductores con las mismas letras también son iguales entre sí. Indica, para los circuitos de esa figura, cómo comprobarías que la diferencia de potencial entre los extremos del grupo de tres resistencias a, b y c no es la misma en el caso del circuito P que en el caso del circuito Q.

Ej7.9. En la figura 7.8 las dos pilas son iguales y los conductores con las mismas letras también son iguales entre sí. Supongamos que la energía que disipa la unidad de carga cuando atraviesa los conductores a, b y c en el circuito Q es de 5 J.

7.9.1. ¿La energía por unidad de carga que atraviesa m y n en el circuito Q será mayor, menor o igual a 5 J?. Justifica la respuesta.

7.9.2. ¿La energía que proporciona la pila en el circuito P a la unidad de carga será mayor, menor o igual a 5 J?. Justifica la respuesta.

8. MODELO MICROSCÓPICO

9. RAZONAMIENTOS CON v, V e I

Llamaremos A, B, C y D a los siguientes conductores

Fig. 9.0

Recordemos que cada pila proporciona la misma energía a cada carga que pasa por ella y que esa energía, la carga la ha de perder por choques fuera de la pila. Si precisa perder más energía en cada choque, estos han de ser más violentos, las cargas deberán ir más deprisa. Si precisa perder menos energía en cada choque, deberán ir más despacio.
Contesta en todos los casos razonando la respuesta, manejando los conceptos de v, V e I

Ej9.1. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. ¿Cómo se moverían si lo conectamos a dos pilas en serie?

Ej9.2. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. ¿Cómo se moverían si lo conectamos a dos pilas en paralelo?

Ej9.3. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. Conectamos el conductor B a otra pila igual ¿Cómo se moverían sus cargas?

Ej9.4. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. Conectamos el conductor C a otra pila igual ¿Cómo se moverían sus cargas?

Ej9.5. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. Conectamos el conductor D a otra pila igual ¿Cómo se moverían sus cargas?

Ej9.6. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. Conectamos otro conductor A´ igual al A en el mismo circuito, en serie con A ¿Cómo se moverían las cargas por A? ¿y por A´?

Ej9.7. Conectamos el conductor A a una pila y las cargas se moverán a una determinada velocidad. Conectamos otro conductor A´ igual al A en el mismo circuito, en paralelo con A ¿Cómo se moverían las cargas por A? ¿y por A´?

Ej9.8. Conectamos el conductor B a una pila y las cargas se moverán a una determinada velocidad. Conectamos otro conductor igual al A en el mismo circuito, en paralelo con la segunda mitad de B ¿Cómo se moverían las cargas por los distintos tramos de B? ¿y por A?

Ej9.9. Conectamos el conductor B a una pila y las cargas se moverán a una determinada velocidad. Conectamos otro conductor igual al A en el mismo circuito, en paralelo con la primera mitad de B ¿Cómo se moverían las cargas por los distintos tramos de B? ¿y por A?

Ej9.10. Supongamos que entre los polos de una pila hay un determinado conductor, uniforme. En un momento dado aumentamos su grosor en una parte. ¿Cómo varían la intensidad de la corriente y las diferencias de potencial de los respectivos tramos?. Toma el modelo D para ayudarte a averiguarlo.

Ej9.11. Supongamos que entre los polos de una pila hay un determinado conductor uniforme. En un momento dado, conectamos en serie otro conductor. ¿Cómo variará la intensidad de la corriente y la diferencia de potencial en el citado conductor?. Toma el modelo B para ayudarte.

Ej9.12. Supongamos que entre los polos de una pila hay un determinado conductor, uniforme y en un momento dado, conectamos en paralelo, entre los mismos polos, otro conductor igual. ¿Se modificarán la velocidad de las partículas?, ¿la intensidad de la corriente?, ¿la diferencia de potencial?.

Ej9.13. ¿Cómo se modifica la intensidad de la corriente en un conductor si en lugar de una pila, conectamos varias pilas iguales en serie?, ¿y en paralelo?

Ej9.14. Supongamos que conectamos a los terminales de una pila un conductor como el C y después, en un tramo del mismo, conectamos en paralelo otro fragmento hasta que quede como el D. ¿Cómo serán la intensidad y la diferencia de potencial en las diferentes partes del nuevo conductor, comparadas con las anteriores?

Ej9.15. ¿Qué pasaría si conectamos un conductor muy corto y muy grueso a una batería?

10. LEY DE OHM

Ej10.1. Diseña un experimento para averiguar si existe la ley que relaciona V e I en los conductores y cuál es.

Ej10.2. Vamos a ver de qué factores depende la resistencia. Pensemos en el modelo microscópico anterior. Hagamos hipótesis y propongamos además experimentos para contrastarlas.

Ej10.3. Dadas dos resistencias, R₁ y R₂, en serie, trata de obtener una expresión para la resistencia equivalente.
Debes utilizar lo siguiente:
a) La diferencia de potencial entre los extremos de la equivalente, será la suma de las diferencias de potencial entre los extremos de R₁ más la diferencia de potencial entre los extremos de R₂.
b) La intensidad que recorra todas ellas es la misma.
c) Se cumple la ley de Ohm para cada resistencia.

Ej10.4. Análogamente haremos con las resistencias en paralelo.
Ahora lo que debes utilizar es lo siguiente:
a) La diferencia de potencial entre los extremos de cada resistencia es la misma, la que proporciona la pila.
b) La intensidad que recorra la equivalente es la suma de las que recorrerán R₁ y R₂.
c) Se cumplirá la ley de Ohm para cada resistencia.

Ej10.5. Una resistencia de 9 Ω se conecta a una pila de 4´5 V, que se comporta idealmente. a) Calcular la intensidad de la corriente que la recorrerá. b) La misma resistencia se conecta a otra pila y medimos una intensidad de 3 A. Calcular la diferencia de potencial entre sus extremos.

Ej10.6. Una resistencia de valor desconocido, cuando se conecta a una pila de 9 V es recorrida por una intensidad de 4 A. a) calcular el valor de la resistencia. b) La misma resistencia se conecta a una pila de 1´5 V. Calcular el valor de la intensidad de la corriente que la recorrerá.

Ej10.7. La resistividad del aluminio es 27´2.10^-9 Ωm. a) Calcular la resistencia eléctrica de un alambre de aluminio de 1 Km de longitud y 2 mm² de sección. b) Si la resistividad del cobre es 16´8.10^-9 Ωm calcular la resistencia eléctrica de un alambre de cobre de las mismas dimensiones.

Ej10.8. Dos conductores cilíndricos p y q, del mismo material, tienen la misma resistencia eléctrica. El conductor p tiene una longitud triple que el q.
a) ¿Cómo son entre sí las áreas de sus secciones transversales?
b) ¿Cómo son entre sí los radios de esas secciones?

Ej10.9. Un trozo prismático de hierro tiene las siguientes dimensiones: 20 cm x 3 mm x 4 mm. Se conecta a un generador que proporciona una tensión de 6 V en el sentido de la dimensión más grande. Calcular la intensidad de la corriente. Resistividad del hierro 10 x 10^-8Ωm.

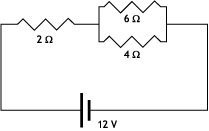
Ej10.10. En el circuito de la figura
a) calcular la intensidad que pasa por la resistencia de 6 Ω.
b) Calcular la diferencia de potencial entre los extremos de la resistencia de 4 Ω.

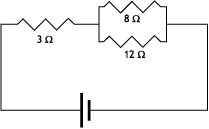
Ej10.11. En el circuito de la figura la intensidad de la corriente que pasa por la resistencia de 8 Ω es de 4 A y el generador es ideal.. Calcular las intensidades y diferencias de potencial en el resto de las resistencias y la fem del generador.

Ej.10.12. En el circuito de la figura el amperímetro 1 marca 8 A y el amperímetro 2 marca 3 A.

a) ¿cuánto marcarán los otros amperímetros?
b) Cortamos ahora el circuito por el amperímetro 2. ¿puedes decir ahora cuánto marcará cada amperímetro?

11. RAZONAMIENTOS SEMICUANTITATIVOS CON R, V e I

Partimos de un circuito, con una pila ideal, cuya diferencia de potencial entre sus extremos es V, la resistencia es R y la intensidad de la corriente que la recorre es I.
Los razonamientos que hagamos estarán basados en la ley de Ohm y en las propiedades fundamentales de la I y de la V.

Ej11.1. Indica razonadamente qué cambios se producirán en el circuito cuando se conecte una resistencia R´ en serie con R.

Ej11.2. Indica razonadamente qué cambios se producirán en el circuito cuando se conecte una resistencia R´ en paralelo con R.
Partimos ahora del siguiente circuito, con una pila ideal, cuya diferencia de potencial entre sus extremos es V, las resistencias R y R´en serie y la intensidad de la corriente que las recorre, I.

Ej11.3. Indica razonadamente qué cambios se producirán en el circuito cuando se conecte una resistencia R´´ en paralelo con R´.

Ej11.4. Indica razonadamente qué cambios se producirán en el circuito cuando se conecte una resistencia R´´ en serie con R y R´.

Ej11.5. Indica razonadamente qué cambios se producirán en el circuito cuando se sustituya R´ por un conductor de resistencia nula.

12. VOLTÍMETROS Y AMPERÍMETROS

Ej12.1. Disponemos de un miliamperímetro de 5 Ω de resistencia interna, que es capaz de medir hasta 8 mA. Calcula la resistencia que se le debe conectar, para transformarlo en amperímetro que mida hasta 8 A.

Ver Resolución de Problemas

Ej12.2. Un voltímetro de 10⁵ Ω de resistencia interna es capaz de medir hasta 20 mV. Calcula la resistencia que se le debe conectar, para transformarlo en voltímetro que mida hasta 200 V.

Ej12.3. ¿Cómo debe ser la resistencia interna de un amperímetro? ¿y de un voltímetro?. ¿Cómo podríamos conseguir cada una de esas cualidades?

Ej12.4. Escribe un breve informe sobre esta cuestión: “El medir perturba el sistema que estamos midiendo”

13. LEY DE JOULE

Ej13.1. Calcular el valor de la resistencia del filamento de una bombilla de 40 W a 220 V.

Ej13.2. Una bombilla tiene la siguiente inscripción: 40 W, 220 V. Calcular la potencia que disipará cuando se la conecte a 125 V, suponiendo que la resistencia no varíe con la temperatura.

Ej13.3. Conectamos en serie, a 220 V, dos bombillas iguales con la siguiente inscripción 60 W, 220 V. Calcular la potencia que disipará cada una en estas condiciones, suponiendo que la resistencia no varíe con la temperatura.

Ej13.4. Conectamos, como indica la figura, tres bombillas de 40 W a 220 V. Calcular la I, V y P de cada una en estas nuevas circunstancias, suponiendo que la resistencia no varíe con la temperatura.

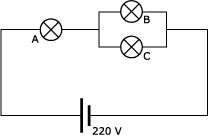Ej13.5. Una estufa eléctrica consume 1000 W cuando se conecta a 220 V.
a) Calcular, en calorías, la energía calorífica que disipará en 8 horas, cuando se conecte a 220 V.
b) Calcular el precio de esa energía
c) Calcular, en calorías, la energía calorífica que disipará en 8 horas, cuando se conecte a 125 V, suponiendo que la resistencia no varíe con la temperatura.

Ej13.6. Una plancha consume 700 W cuando se conecta a 220 V
a) ¿Cuál es su resistencia eléctrica?
b) ¿Cuánto dinero se gasta al estar planchando 2 horas, conectada a 220 V?
c) ¿Cuál sería la potencia consumida si se conecta a 125 V, suponiendo que la resistencia no varíe con la temperatura?.
Utilizar como precio del kW h, 0´083007 €/kW h

Ej13.7. Supongamos que el generador es de 220 V, que la bombilla es de 100 W, 220 V y que el cable es de cobre, de sección circular y de 1 km de largo y 0´5 mm de diámetro. Calcular la potencia que se disipará en la bombilla, suponiendo que su resistencia no depende de la temperatura. Dato: resistividad del cobre, 16´8.10^-9 Ωm

14. GENERADORES DE CORRIENTE

Ej14.1. En el circuito de la figura calcular las intensidades de la corriente y diferencias de potencial en todas las resistencias. Calcular también la diferencia de potencial entre los extremos de la batería.

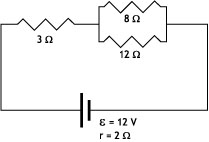Ej14.2. En el circuito de la figura, un voltímetro marca 20 V entre los terminales de la pila cuando el circuito está abierto y 19´5 V cuando el circuito está cerrado. Si la resistencia externa es de 100 Ω, calcula la resistencia interna y la intensidad.

CUESTIONES DE EVALUACIÓN

A continuación se proponen unos ejemplos de cuestiones de evaluación. En las de opción múltiple después de cada pregunta se dan varias respuestas posibles, de las cuales solo una es correcta, y esa es la que debes elegir. Abreviadamente nombramos la diferencia de potencial, como d.p.

E1. En el circuito dado en la figura, la lectura del amperímetro es I. Una resistencia adicional R´se conecta, en paralelo con R, entre M y N. En consecuencia:
a. La lectura I no cambia y las corrientes en R y R´son inversamente proporcionales a sus resistencias
b. La d.p. entre M y N no cambia.
c. La lectura I crece y la d.p. entre M y N decrece.
d. El calor desarrollado en R no cambia.
e. La lectura I crece y la d.p. entre M y N crece.

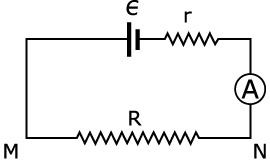E2. La fuente de voltaje no tiene resistencia interna. Ambas bombillas M y N están luciendo. Quitamos N de su casquillo. Consecuentemente:
a. La bombilla M lucirá más fuertemente.
b. La diferencia de potencial entre C y D se hará cero.
c. La diferencia de potencial entre C y D no cambiará.
d. La diferencia de potencial entre C y D aumentará.

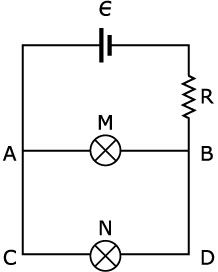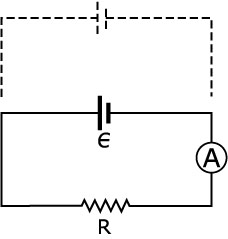
E3. La lectura del amperímetro en el circuito dibujado en la figura indica una cierta corriente. La batería no tiene resistencia interna. Conectamos una segunda batería idéntica a la primera, en paralelo con ella, como indica la figura. Consecuentemente:
a. La lectura del amperímetro aumentará.
b. La diferencia de potencial entre los extremos de R aumentará.
c. La corriente que fluya a través de la primera batería disminuirá.
d. La corriente que fluya a través de la primera batería no cambiará.

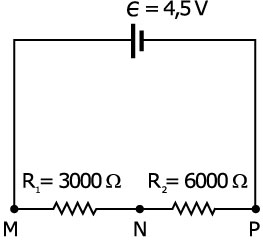
E4. Dos resistencias R₁ y R₂ están conectadas en serie a una batería que no tiene resistencia interna, y una f.e.m. de ε= 4´5 V. (ver figura)
a. ¿Cuál es la d.p. entre los puntos M y N y cuál es la d.p. entre los puntos N y P?
b. Un voltímetro con un rango total de 3 V se conecta entre M y N y marca 0´9 V ¿cuál es la d.p. entre los puntos N y P ahora? ¿Por qué los valores ahora son diferentes a los que has calculado?

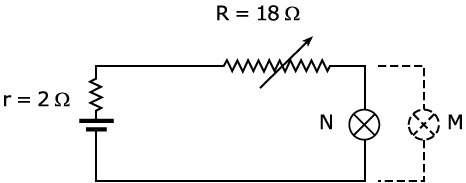
E5. En el circuito dibujado en la figura, una bombilla N se conecta a través de un reóstato a una batería que tiene una resistencia interna de 2 Ω. Cuando el reóstato se fija a 18 Ω, la bombilla luce normalmente. Ahora, una segunda bombilla M, idéntica a N se conecta en paralelo con ella. El reóstato se reajusta de modo que ambas bombillas luzcan con la misma intensidad con que N lucía previamente. ¿a qué resistencia ha reajustado el reóstato?