| [LA LEY DE JOULE] |
Esta ley relaciona la potencia disipada por una resistencia con el valor de dicha resistencia y la intensidad de la corriente que la recorre.
Recordemos la relación entre P e I que es P=VI (esta relación proviene de la misma definición de los conceptos V e I: V es la energía que pierde la unidad de carga e I el número de cargas por unidad de tiempo, luego el producto será la energía que pierden todas las cargas por unidad de tiempo)
Consideremos el conductor representado en la figura por cuatro iones positivos.
Entra un electrón a chocar con el primer ión, En ese momento, todos los electrones se desplazan hacia la derecha y realizan un choque con el ión correspondiente. Ha habido cuatro choques con iones del conductor considerado (el último, el que sale, no choca con uno de los cuatro iones del conductor que nos interesa). Por tanto, por cada electrón que entra hay un número de choques igual que si ese electrón hubiera hecho todo el recorrido por el conductor hasta salir de él, esto es, por cada unidad de carga que entra hay una pérdida de energía eléctrica en el conductor igual a V, correspondiente a un recorrido completo de la misma por el conductor V sería esa pérdida de energía en un recorrido completo de la unidad de carga).
13.1 Deducción teórica de la ley de Joule
Partimos de la relación P=VI
Por otro lado consideramos la ley de Ohm, V= IR.
Eliminamos V entre las dos ecuaciones para obtener la ley que buscamos.
P=I2 R
Ya obtuvimos un adelanto de esta ley en el apartado 5, cuando comprobamos que la potencia disipada debía ser proporcional al cuadrado de la intensidad.Podemos ver el artículo original de Joule en el que relata su descubrimiento H5 La ley de Joule
Notemos que Joule obtuvo esta ley experimentalmente y que pensó que, utilizarla para medir intensidades a base de medir calores por unidad de tiempo, producidas por una resistencia, podría ser una posible aplicación de la misma, aunque de momento la desechó porque el error en la medida de calores era muy superior al cometido por los amperímetros utilizados en su época.
Expresiones equivalentes son:
P = V2/R = I2R = VI
Energía disipada en una resistencia
Puesto que P = E/t,
E = Pt = (V2/R)t = I2Rt = VIt
En la ciencia se pueden jerarquizar las leyes de modos diferentes. En esta deducción hemos partido de P = VI (la potencia como una función de V), y en el apartado de conceptos básicos vimos que podía medirse la diferencia de potencial V = P/I, a partir de la potencia disipada. Ya hemos dicho anteriormente que son más importantes las relaciones entre los conceptos que las demostraciones.
13.2 Deducción empírica de la ley de Joule
A13.2 Diseña un experimento para comprobar empíricamente la ley de Joule. Puedes ver una respuesta en el texto en el que Joule describe sus experimentos a este respecto.
Puedes hacer los ejercicios 13.1 al 13.6
13.3 Pérdidas de energía en las líneas de transmisión
Imagina que tienes un circuito con un generador y una bombilla,
 |
pero el generador se encuentra muy lejos de la bombilla. Para conectarlos necesitamos un cable muy largo
con lo cual tendrá una resistencia, tanto el cable de ida como el de vuelta, esto es, el que está conectado en un terminal de la bombilla y del generador y el que está en el otro terminal de la bombilla y del generador.
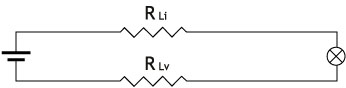 |
La bombilla tiene una resistencia y los cables, al estar en serie, podemos considerar, por sencillez que tienen otra, que es la suma de las de ambos. El esquema queda como sigue.
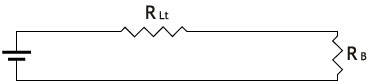 |
Cuando la bombilla y el generador estaban cerca, se disipaba potencia en la bombilla, únicamente. En este caso no es despreciable la potencia que se disipa en los cables.
Puedes hacer el ejercicio 13.7
<<ANTERIOR SIGUIENTE >>